مثال) مساله زیر را در کمترین زمان ممکن حل کنید.

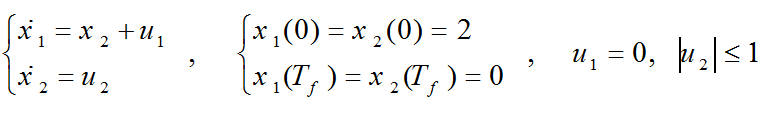
پیش از شروع حل مساله به شرح و بسط مفهوم این سوال می­پردازیم. در اینجا یک دستگاه معادلات دیفرانسیل معمولی وجود دارد با دو متغیر و مشتقاتشان. و قصد نهایی ما کنترل کردن این دستگاه و رساندن آن به یک نقطه ی مطلوب در حداقل زمان ممکن است. حال بیایید بر نیروهای ورودی u تمرکز کنیم. همانطور که مشخص است، کنترل دو متغیر، با استفاده از دو نیروی ورودی بسیار آسان تر از حالتی است که یک نیروی ورودی داشته باشیم. این مثال را در نظر بگیرید: اگر بخواهیم موقعیت یک خودرو را کنترل کنیم، در حالتی که فقط پدال گاز آن کار می­کند، عمل کنترل به مراتب دشوارتر از حالتی است که پدال ترمز نیز در دسترس باشد.

لم1) توضیحات بالا مقدمه ای است بر اینکه این مطلب را بیان کنیم: هرچند که نیروی ورودی  درصورت سوال برابر با صفر قرار گرفته است، اما اگر این عبارت را چیزی مانند ε (مقداری بسیار کوچک) فرض کنیم، علاوه بر اینکه در صورت سوال تغییری به وجود نیامده است، حل مساله نیز آسان گشته است. حال بیایید راه حل را بررسی کنیم:

در اینجا با مساله بهینه سازی یک انتگرال (در اینجا زمان) و یک قید (در اینجا معادلات دیفرانسیل) مواجه هستیم. دقت کنید که مینیمم کردن زمان حل به معنی حداقل بودن انتگرال زمان پاسخ است. و این انتگرال باید در شرایط ارضای دستگاه معادلات دیفرانسیلی موجود در صورت سوال، مینیمم شود. برای این دست مسایل، تابع همیلتونی ترکیب از این دو (معادله زیر انتگرال و معادلات قیدی) به صورت زیر تشکیل میشود.

که در آن به  بردار شبه حالت ها یا بردار متغیرهای لاگرانژ میگویند. این متغیرها مجهول بوده و طی فرایند بهینه سازی تعیین می­گردند. دقت شود که در اینجا با مساله مینیمم سازی فرایند حل مواجهیم. پس انتگرال هزینه برابر است با:

با اضافه کردن معادلات قیدی (دستگاه معادلات دیفرانسیلی) به عبارت بالا داریم:

شرایط بهینه بودن برای تابع همیلتون بالا چنین است:

که در آن، بالا نویس * به معنی حالت اپتیمم است. وقتی که زمان نهایی حل مشخص باشد، روال حل مساله آسان خواهد بود. پس بیایید سوال را تبدیل به یک مساله در زمان مشخص کنیم. ایده حل این است که زمان  نهایی حل (زمان بهینه) را به صورت یک پارامتر در سوال وارد کنیم و سوال را در بازه زمانی [0-1] حل کنیم. با درنظر گرفتن زمان کنترلی نهایی به صورت یک متغیرحالت، و تغیر متغیر  به جای t ، معادله 4 را می­توان چنین نوشت:

همانطور که مشخص است، عبارت بالا یک دسته معادلات دیفرانسیل است که باید با توجه ورودی کنترلی مناسب حل گردند. حال سوال اینجاست که این ورودی کنترلی چگونه تعیین میگردد. برای مسایلی که زمان حل مشخص است، ورودی کنترلی چنین به دست می­آید:

عبارت بالا به یک معادله جبری منجر می­شود که از آن، نیروهای کنترلی را میتوان بر حسب  یافت. معادله 6 را بازنویسی می­کنیم:

اما همانطور که مشخص است، در معادله 7 هیچ اثری از ورودی های u ظاهر نشد. برای رفع این نقص، به یک تغییر متغیر میپردازیم. با استفاده از لم1 میتوان نوشت:

با توجه به شرایط نیرویی که در صورت سوال آمده است () می­توان عبارات زیر را جایگزین نمود:

پس رابطه 3 به صورت زیر خواهد بود:

و از آن رابطه 7 را به صورت زیر می­توان محاسبه کرد:

معادله جبری 11 به پاسخ زیر منتهی می­شود:

 پس رابطه 9 چنین است:

پس دستگاه معادلات 5 به شکل زیر است:

همانطور که گفته شد، بازه زمانی حل سوال به [0-1]  تغییر یافت. پس معادلات مرزی مساله نیز به حالت زیر خواهد بود:

اما دستگاه معادلات 14، از بعد 5 بوده پس به 5 شرط مرزی نیاز دارد. با توجه به محدودیت نیرویی صورت سوال، شرط مرزی پنجم چنین انتخاب می­گردد:

با توجه به رابطه 12 داریم:

پس در نهایت 5 شرط مرزی چنین است:

و در نهایت، پاسخ چنین است: